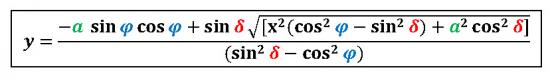CORNILLAC en Drôme Provençale
Association pour la sauvegarde du patrimoine de Cornillac
Cadrans solaires
L'observation de la variation de l'ombre d'un objet au cours de la journée et au cours de l'année a très vite suggéré aux hommes que l'on pouvait utiliser le Soleil comme repère du temps.
Anaximandre de Milet (610 - 547 Av. J.C.), philosophe, mathématicien et astronome grec, né à Milet. Ami et disciple de Thalès de Milet , il a laissé très peu de documents mais aurait apporté aux Grecs le gnomon (cadran solaire ) utilisé pour la mesure du temps par les Babyloniens .
Vitruve Marcus Vitruvius Pollio, connu sous le nom de Vitruve, est un architecte romain qui vécut au Ier siècle av. J.-C. L'Analemme de vitruve
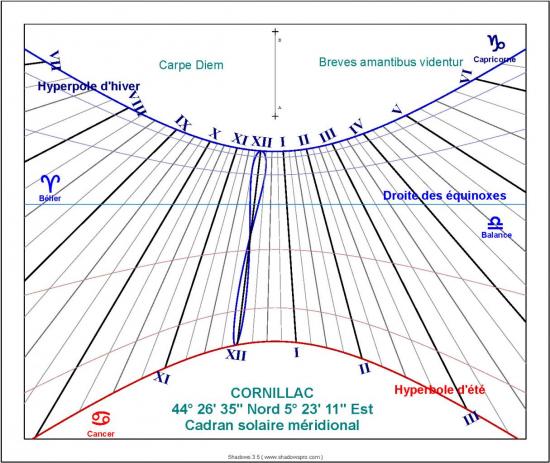
Simulation d'un cadran solaire vertical méridional
à Cornillac
Tracé des hyperboles sur un cadran méridional
La courbe décrite par l'extrémité de l'ombre d'un gnomon, mise sous la forme y = f (x), s'écrit :
Calcul de la déclinaison du soleil
Jour de l’année : J (1 à 365)
Anomalie moyenne : M = 357°+0°,9856*J
Equation du centre : C = 1°,914*Sin(M)+0°,02*Sin(2*M)
Longitude vraie du soleil : L = 280°+C+0°9856*J
0,9856 déplacement quotidien moyen de la Terre sur son orbite autour du Soleil
Réduction à l'équateur : R = - 2°,466*Sin(2*L)+0°,053*Sin(4L)
Sin(déclinaison) = 0,3978*Sin(L)
0,3978 sinus de l'obliquité de l'éclitique
CADRAN SOLAIRE VERTICAL MERIDIONAL
Equinoxe de printemps
Solstice d'été
Equinoxe d'automne
Solstice d'hiver
Solstice d'hiver
21décembre
Date de dernière mise à jour : lundi 05 juillet 2021